Mise en œuvre de la théorie des graphes pour la circulation des agents

Objectif: Faire passer les véhicules par les routes en empruntant le plus court chemin
Entrée : Cellule de départ, cellule d’arrivée et un tableau pour contenir le plus court chemin
Sortie : Le tableau contenant le plus court chemin et la distance en cellule de ce chemin
Outils : Repast-Simphony et les modules nécessaires à son fonctionnement

Notion de graphe non étiqueté et plus court chemin dans un raster

Une arête relie deux sommets successifs (qu’ils soient visibles ou pas). Et dans un graphe non étiqueté toutes les arêtes ont même longueur.

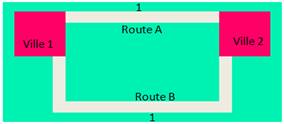
Si nous considérons le graphe suivant (figure 1) : ville 1 et ville 2 sont les seuls sommets et il n’y a que deux (2) arêtes, routes A et routes B. Utiliser les graphes non étiquetés ne nous permet donc pas de savoir le plus court chemin entre ces deux routes car chacune vaut 1. C'est donc exactement la même chose de passer sur la route A que sur la route B.

Figure 1 : Graphe à 2 sommets

Mais si nous considérons le graphe si dessous (figure 2), en considérant que chaque cellule des villes et des routes est un sommet et que la distance entre deux nœuds successifs (arête) est égale à l’unité (1), alors nous pouvons bien faire la différence entre la route A et la route B. En effet, de la cellule α à la cellule β, la longueur de la route A est 17 (16 + 1) et celle de la route B est 27 (26 + 1). Ce graphe a 66 sommets (toutes les cellules rouges et gris claires).

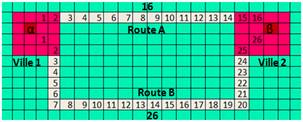
Figure 2 : Graphe à 66 sommets

Suivant cette logique, nous avons utilisé la grille pour construire notre graphe non étiqueté tout en prenant en compte les distances (figure 3).

Figure 3

Construction et utilisation des graphes

Pour que les véhicules puissent passer par les routes et en empruntant le plus court chemin, on a utilisé la théorie des graphes. Ainsi nous avons créé principalement deux classes qu’utilisent les agents transporteurs (C_HumanCarrier) pour trouver un plus court chemin et le parcourir (Figure 1):

Figure 1 : Diagramme des classes UML pour le graphe

1- C_UnweightedGraph : c’est la classe de base encapsulant toutes les données se présentant sous forme de graphe non étiqueté (voir mémo). Elle contient principalement :

· Un tableau pour contenir les références de tous les nœuds du graphe,

· Une matrice d’adjacence (carrée, booléenne) de taille: le nombre de nœuds du graphe. Elle nous permet de connaître l’adjacence entre deux nœuds,

· Une méthode Dijkstra nous permettant de connaitre le plus court chemin entre un nœud et tous les autres nœuds du graphe,

· Une méthode faireChemin nous permettant de construire à partir de Dijkstra le plus court chemin entre deux sommets du graphe.

2- C_RasterGraphManager : une classe qui dérive de C_RasterManager (chargé de la gestion du sol), ici on a :

· Une méthode makeTracksGraph permettant d’instancier et de construire l’objet ou les objets graphe de type C_UnweightedGraph c’est à dire renseigner le tableau des nœuds et la matrice d’adjacence. Pour chaque graphe, cette méthode n’est exécutée qu’une seule fois,

· Une méthode buildPath permettant de construire un plus court chemin entre deux sommets du graphe (entre deux endroits de la carte). Cette méthode est appelée à chaque fois qu’un HumanCarrier veut construire un plus court chemin entre l’endroit où il se trouve et l’endroit où il veut aller,

· Une méthode selectNextNode permettant de parcourir les chemins. Un chemin est constitué de plusieurs nœuds et à chaque fois que le HumanCarrier arrive à un nœud, il appelle cette méthode pour qu’elle lui indique le nœud suivant.

Mémo 26 - Auteur P.A. Mboup, 03.10.13

retour aux mémos retour au modèle retour à la page d'accueil